Google CTF 2020 [.Net-RE]

CTF Writeups
, , ,
banner

I got to know that Google CTF had some interesting rev challs. I was late for it so I didn’t participate in the event with a team and also we aren’t quite active these days.
I picked up 2nd least solved reversing challenge ie. .Net. Its an interesting challenge and I learnt a lot from it as well, so it might be a little longer than usual but its worth it in the end.

Challenge

.Net is great, especially because of all its weird features.
Download : chall.zip

TL;DR

  • Dynamic Instrumentation using HarmonyLib
  • C# <=> Native asm FFI
  • IDAPython Scripting to assist in native functions analysis
  • Replicate algo in python and then finding a valid solution for it using z3

Introduction

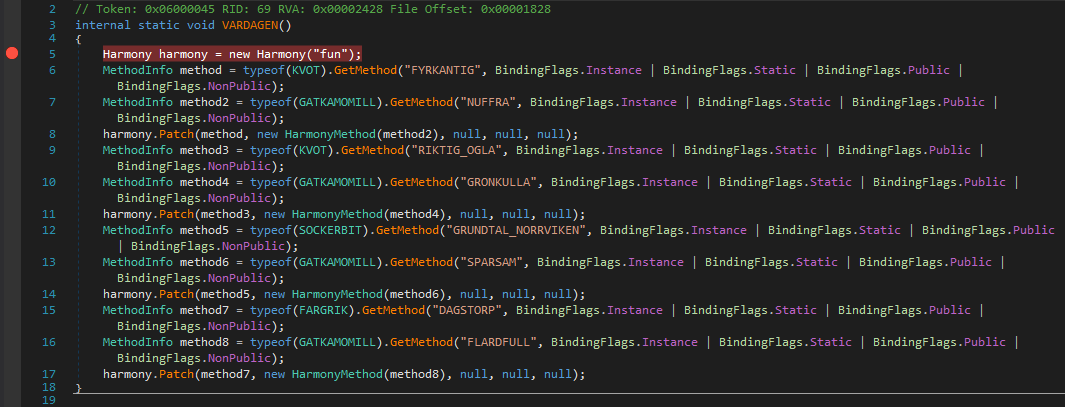
The challenge includes two files ie. 0Harmony.dll and EKTORPFlagValidator.exe.
So the name looks a bit weird. I just googled them and found that Harmony is actually a libary for doing some runtime patching stuff in .Net apps.

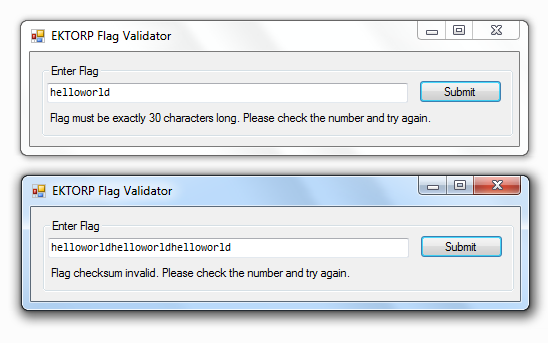
With the help of a sample run, we see that it requires a string of length = 30 and also that it validates a checksum from our input.

sample_run

Static Analysis

So lets start at the entrypoint. And yeah at first I tried to analyse the constructor too but it looked kinda hard to understand statically and I left it for debugging at last.

entrypoint

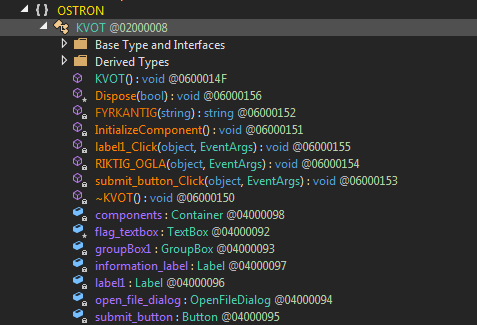
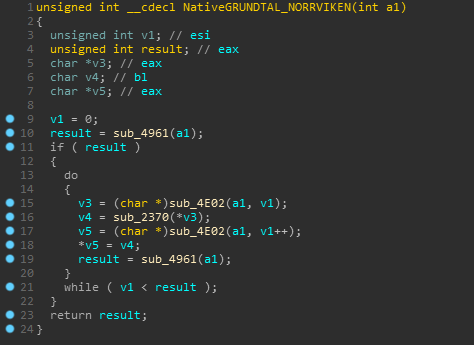
So there is this main method which later calls LaunchGui() and as a result we are now in KVOT class.

main

launchgui

Now we are inside KVOT and it looks like method names are weird.

kvot

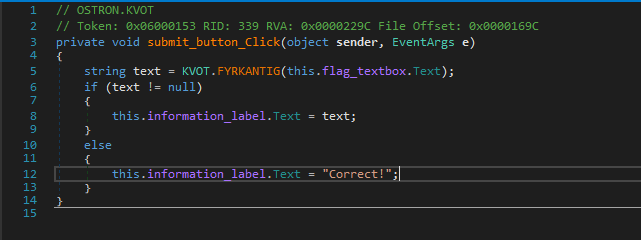
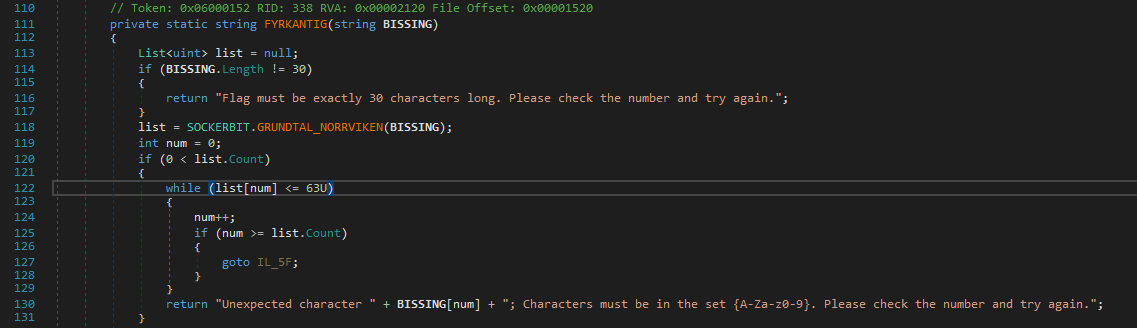
After the basic initialization part for the GUI there is an event handler submit_button_Click() which looks exactly how we want it to be.

submit

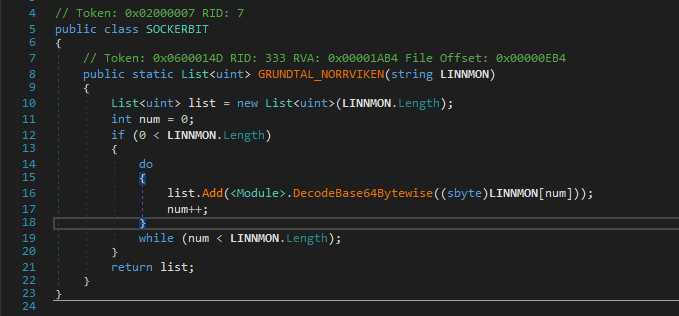
Ahmmm It does the string length check here, and if it succeeds then call another method with our input string as an argument to SOCKERBIT.GRUNDTAL_NORRVIKEN which returns a list.
Also after that it does a basic check that the elements of the returned list are all less than 63 which looks like a character range check from the failure string.

main_check1

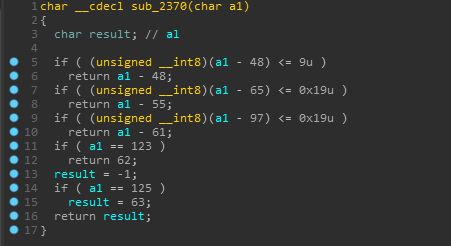
And yeah, There is more to it, just hold up.
GRUNDTAL_NORRVIKEN then calls DecodeBase64Bytewise on each of the element of our string.

enc_char

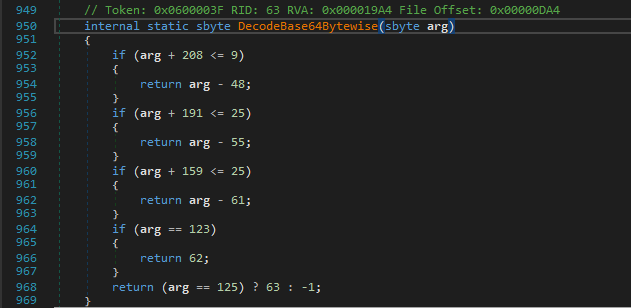
Hmm, now it gets weird… the DecodeBase64Bytewise method looks like it is trying to instead encode our input and also it checks some conditions which would never return true except the 123('{') and 125('}') check.

decodebase64bytewise

That means if we input some lowercase characters which should be valid, then it’ll just return a list of 30 -1’s.

drawing

But the signness trick here casts it to an unsigned integer.
Something like this : 

1
2
3
4
5
if ((uint)(byte)(arg + 191) <= 25u)
{
  Console.WriteLine((uint)(byte)(arg + 191));  // overflows  
  return (sbyte)(arg - 55);
}

For eg. ‘H’(72) fulfills the above condition since (byte)(72+191) is 7 when cast to a byte and not 263.

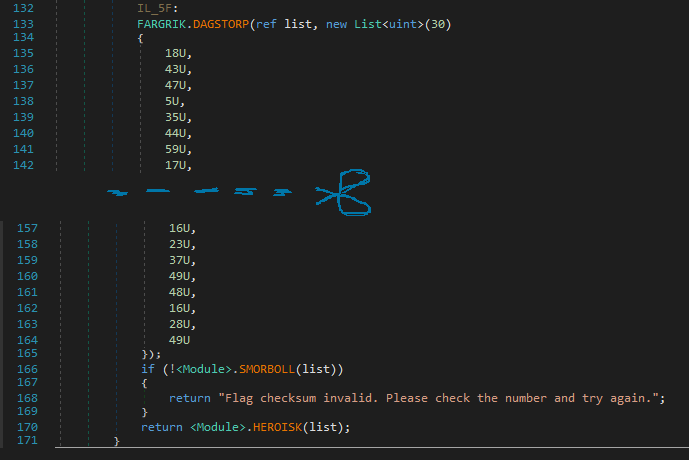
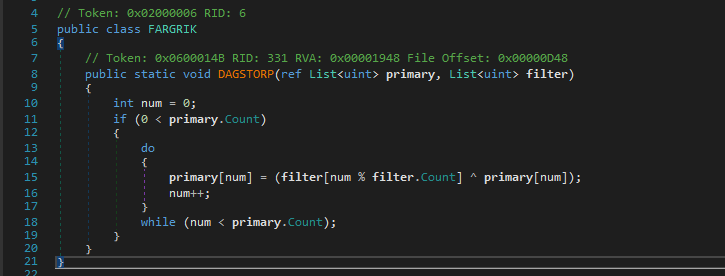
This is the 2nd part of the check routine with methods DAGSTORP, SMORBOLL and HEROISK.
A list is initialized and passed to DAGSTORP along with our encrypted input.

main_check2

Ahh, It just looks like a simple xor, ezpz!

list_xor

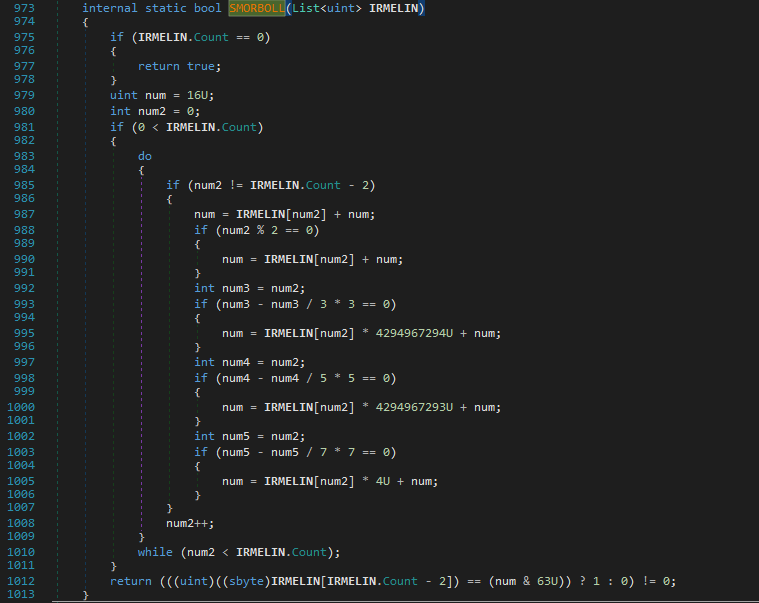
Then there is this checksum as you’ve guessed it from the failure string. It calculates the checksum on the basis that it does different calculations according to the index value.
The index value checks are just for checking whether the index is divisible by 2,3,5 or 7 and FYI, it doesn’t include the index 28 as it is later compared with the final checksum value.

checksum

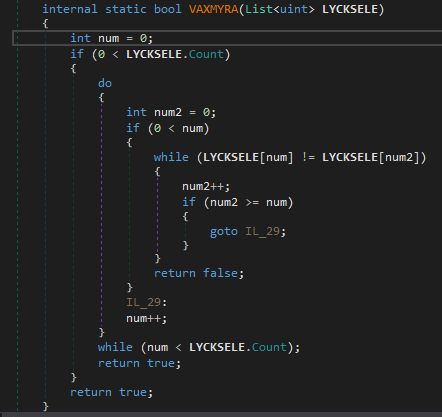
And then there is method VAXMYRA which just checks if there are any duplicates in the encrypted array.

vaxmyra

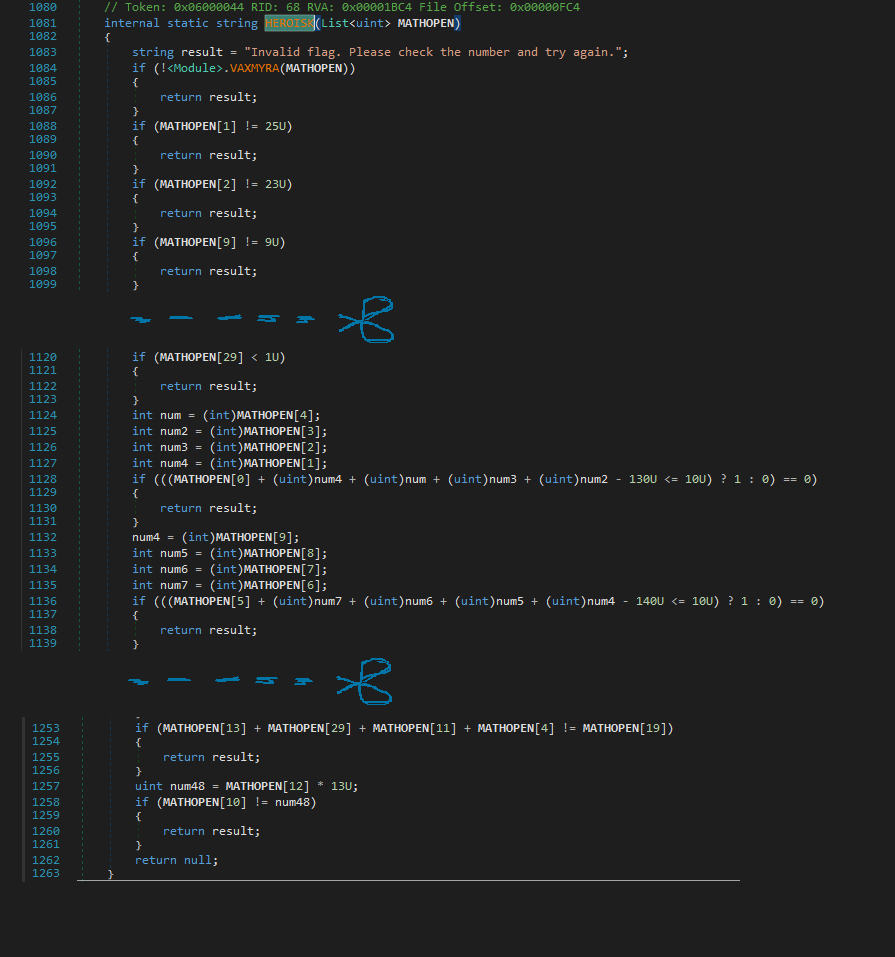
And after bypassing through the checksum validation and VAXMYRA we get to the main condition checks that validates our encrypted input. And Yes, I smell z3!

final_conds

Dynamic Analysis

Getting to the main fun part ie. debugging it in dnsPy.
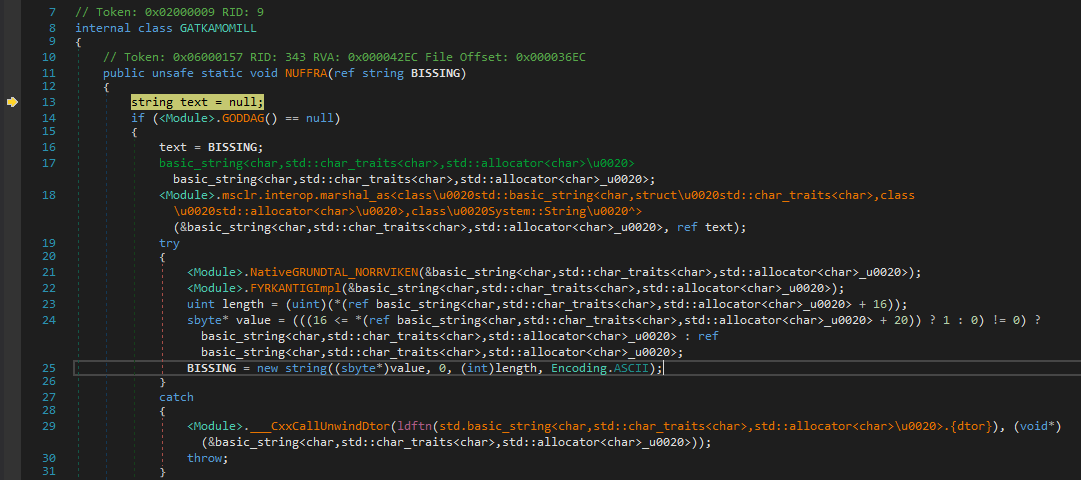
Huh wait a sec where is FYRKANTIG. Instead we get redirected to NUFFRA and now it looks more complicated and gibberish to deal with.

nuffra

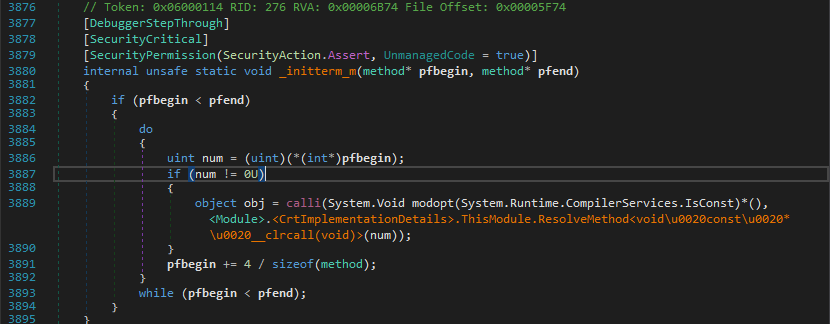
So to explain this inner magic and so called weirdness we’ll have to debug right from the constructor. If you’d traced the execution accurately, you’ll find that there is a calli instruction which calls a method by specifying its address as an argument.

calli

I noticed that it calls several functions and just noted down the method addresses ie. from num variable. 

1
2
3
4
5
6
7
8
9
10
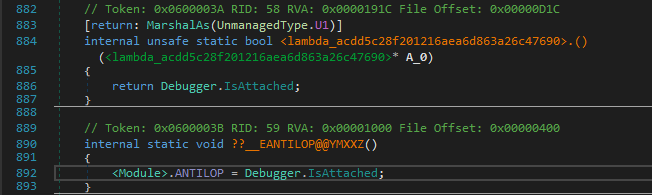
11
0x600003B   # Debugger.IsAttached() check (native)
0x600003D
0x6000046   # patch functions routine (native)

0x60000D6
0x60000D7
0x60000D8
0x60000D9   # we don't care about the 0xD6-0xDC functions
0x60000DA
0x60000DB
0x60000DC

0x600003B has a simple anti-debug check with System.Diagnostics.Debugger.IsAttached!

is_debugger_attached

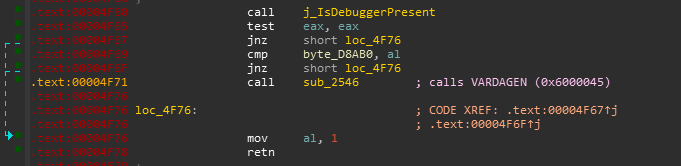
0x6000046 is the magic method here which in turn calls another native function.

harmony_caller

That native function has another anti-debug technique implemented ie kernel32.dll::IsDebuggerPresent and if it is true it returns 1 which eventually doesn’t do anything and the latter will call a c# method which is indeed responsible for changing the methods.

debugger_check1

And Fortunately it happens that dnsPy has got us covered and was successful in deafeating those anti-debug techniques like a ninja. All thanks to this issue

Harmony Magic

So this is the function called if the isDebuggerPresent returns false and it looks like it is patching the original methods we found during the static analysis to some other methods.

patched_fcns

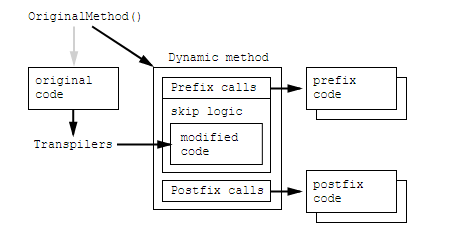
How Harmony works

Harmony docs explains it better but basically here it just patches a method body at runtime.

From docs :
Where other patch libraries simply allow you to replace the original method, Harmony goes one step further and gives you:

  • A way to keep the original method intact
  • Execute your code before and/or after the original method
  • Modify the original with IL code processors
  • Multiple Harmony patches co-exist and don’t conflict with each other

harmony_logic

As a reference we can have this Patched Method List :

Original method Patched Method
KVOT.FYRKANTIG
(static fcn caller)		 GATKAMOMILL.NUFFRA
(native fcn caller)
KVOT.RIKTIG_OGLA
(useless)		 GATKAMOMILL.GRONKULLA
(useless)
SOCKERBIT.GRUNDTAL_NORRVIKEN
(DecodeBase64ByteWise() caller)		 GATKAMOMILL.SPARSAM
(str to list convertor)
FARGRIK.DAGSTORP
(xor implementation)		 GATKAMOMILL.FLARDFULL
(anti-debug check [GODDAG])

Analysing Native Functions with IDAPython

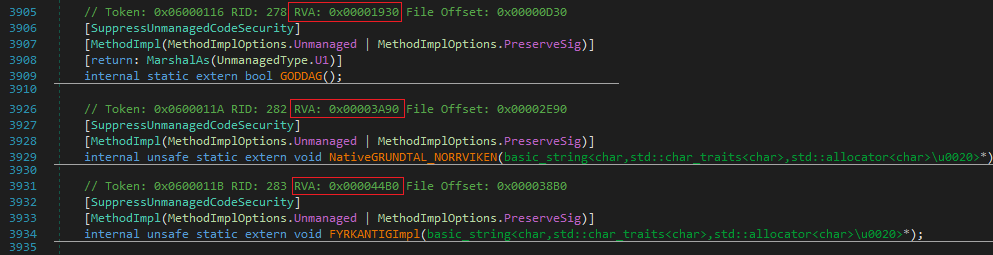
Digging Deeper we need to analyse these native functions in some dissasembler like IDA, as dnsPy fails for them. These are the three main native functions called by method NUFFRA. Also, note down the RVAs marked in Red, these are the references to the native functions.

native_fcns

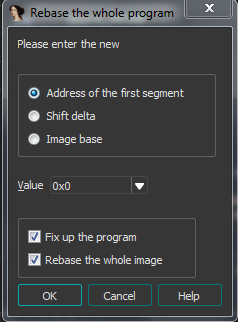
In IDA, we should load it as a normal PE file and then define some code at different locations as IDA doesn’t recognise it very well. Here we can either rebase the program to make it try to load from 0x0 or add 0x400000 to the RVA and then analyse it.

rebase

  • Func 1 [GODDAG]

We can just go over that address (0x00001930) and defining it as code pretty much clears what is it used for. So there is a anti-debug check, and this looks like the right function as well since it returns True/False, which is then used in the C# code to progress further if False.

debugger_check2

  • Func 2 [NativeGRUNDTAL_NORRVIKEN]

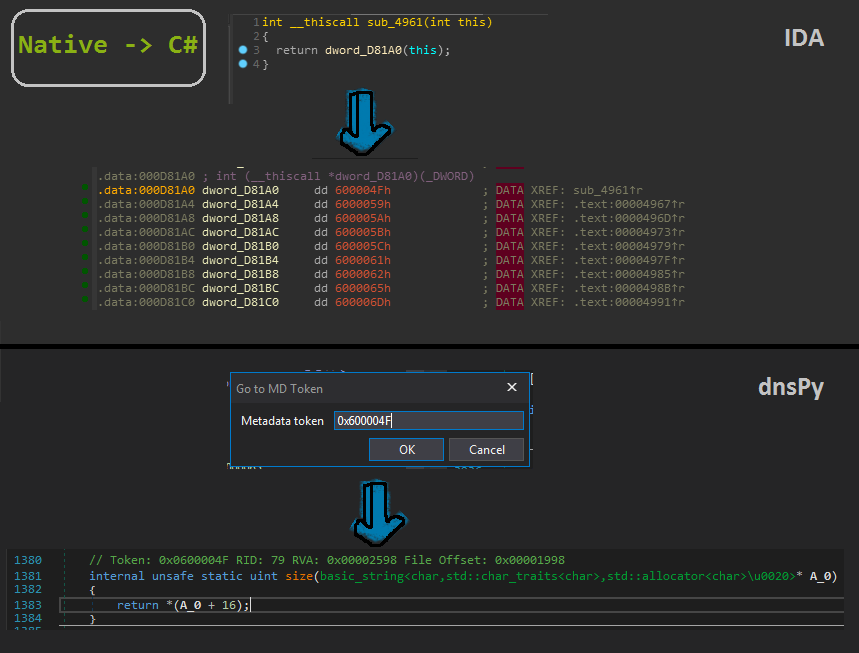
The second important function is performing some functions on our input string elements.

native1

Now this native function is interesting as the defined functions are just dwords and If we observe these are just referencing the C# code instead.

This can be illustrated by the following :

native_to_cs

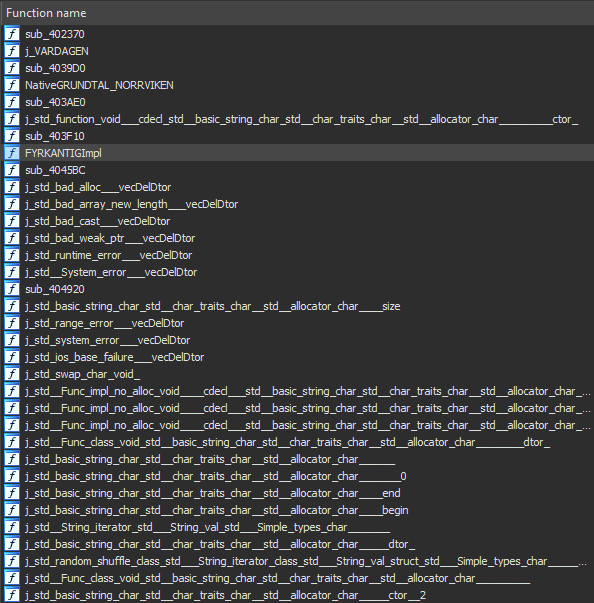
For automatically renaming these dwords we first we need to navigate to Storage Stream -> Method to get a full list of methods.

storage_stream

We can then copy them, make a json file with token and method names as the keys and values respectively. Now we can write an IDAPython script to rename the dwords recognised by IDA with the name as ‘dword_xxxx’ accordingly.
TBH this idea of scripting IDA struck to me while doing this writeup lol. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def rename_dwords():
  f = open('method_map.json') 
  method_map = json.load(f) 
  token_list = [int(x,16) for x in method_map.keys()]

  data_seg_selector = idc.SegByName('.data')
  data_seg_startea = idc.SegByBase(data_seg_selector)
  data_seg_endea = idc.SegEnd(data_seg_startea)

  #maybe compability issue
  SN_FORCE = 0x800

  for ea in range(data_seg_startea, data_seg_endea):
    var_name = Name(ea)
    if 'dword' in var_name:
      dword_val = Dword(ea)

      if dword_val in token_list:
        formatted_token = "0x0%X" % dword_val
        new_name = str(method_map[formatted_token])
        idc.set_name(ea, new_name, SN_NOCHECK | SN_FORCE)
        print "done renaming " + var_name +" to " + new_name

Ahh We get a nice and clean view of all the renamed referenced dwords as functions though I’ll not refer to this renaming fashion in this writeup since it is not the best way to make a third person understand the algo as afterall it has method names which will be long af along with their class which we don’t care about here.

ida_script_res

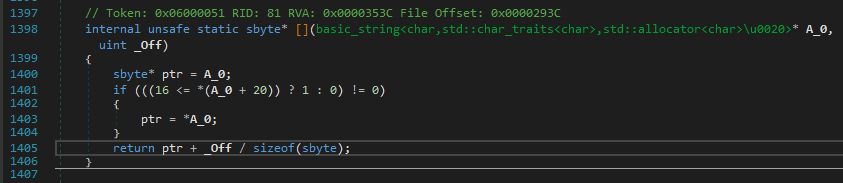
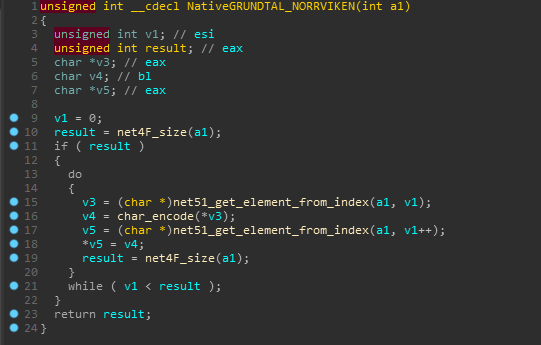
Continuing with the analysis of NativeGRUNDTAL_NORRVIKEN, we see some offset calculations and dereferencing a pointer from that offset and later returning it.

net51

Yes! This looks like the main encryption algo. This checks if the character is in the valid chars range and then encrypts it. The last two checks are similar for curly braces.

char_encode

And after some renaming, the NativeGRUNDTAL_NORRVIKEN function looks like the following which concludes that it is only used for encrypting the string.
Also FYI, it uses another list for storing the encrypted string as there is another get_element_from_index func.

native1_renamed

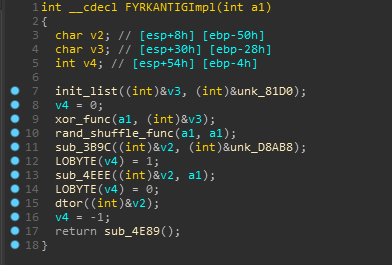
  • Func 3 [FYRKANTIGImpl]

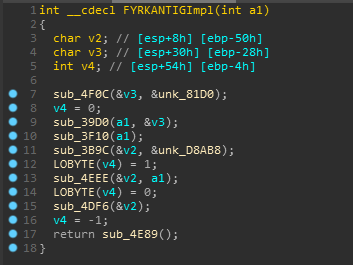
native2

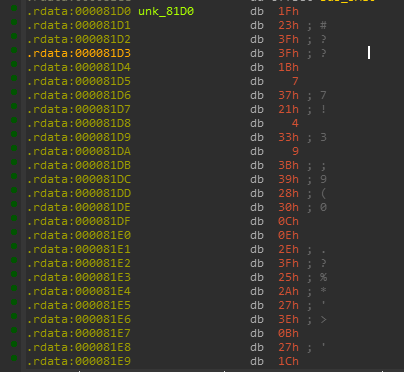
So There are two vars used from the .rdata section in the function, one of them is an array and other one doesn’t look interesting as it is a stack variable.

xor_arr_data

The function which uses is referenced in C# and looks like it is just used to initialize the array.

xor_arr_init

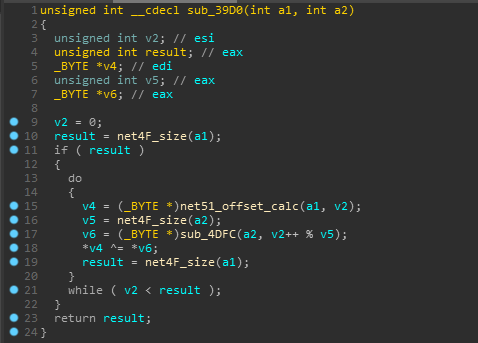
And yeah we get that xor function in sub_39D0 and FYI sub_4DFC is same as net51_offset_calc.
So till now It has xored our encrypted input with the array it just initialized.

xor_native_fcn

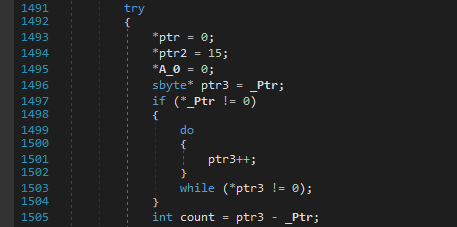
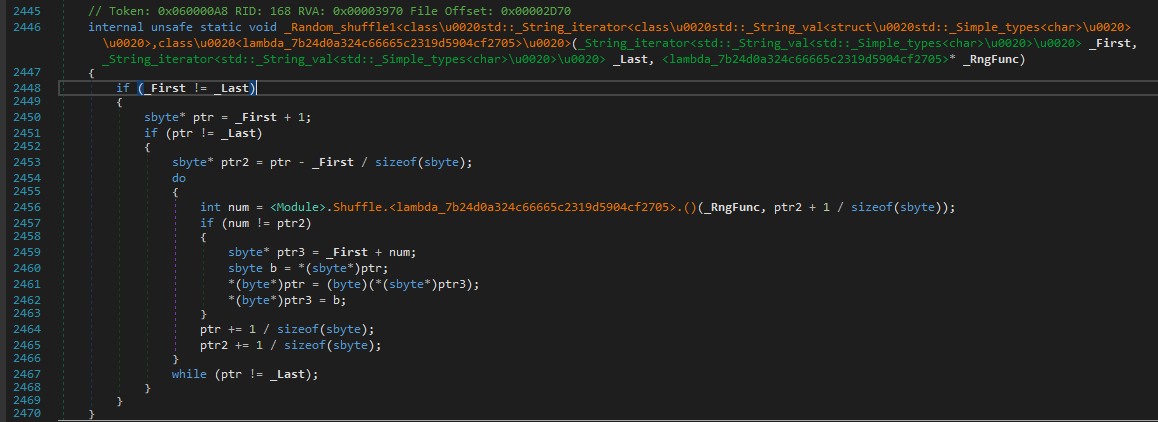
Moving on, we can clearly see that sub_3F10 is used for performing some random shuffling on the resulting xored array.

random_shuffle_net

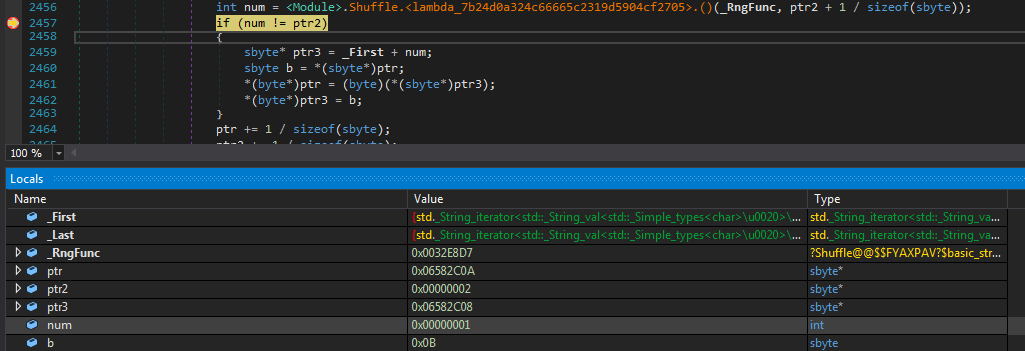
There is no point in wasting time on analysing it as we can just note the num ie. the offset (randomly generated but seeded with a static value) by setting the breakpoint as shown below and watching its value on every iteration which makes some swaps with the encrypted input list.

rand_shuffle_debug

This is what the native function looked after renaming some stuff.

rand_shuffle_func_renamed

So the main algo of FYRKANTIGImpl is just to xor and random shuffle our encrypted input. I’ve renamed some other functions now for better understanding.

native2_renamed

We can also script some part of defining and renaming functions just from their RVAs.
This also let me think that this can be implemented into a plugin package. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def define_functions():
  native_rvas = [0x1930, 0x3A90, 0x44b0,]
  native_rvas = [(0x400000 + x) for x in native_rvas]

  for ea in native_rvas:
    if ea == 0x401930:
      # undefine and force convert to code as IDA doesn't analyse it at first
      print "Defining fcn GODDAG at 0x%x" % ea
      print "Making", ea, "unknown and defining it to code..."
      idc.MakeUnkn(ea,1)
      idc.MakeCode(ea)
      idc.MakeUnkn(ea+8,1)
      idc.MakeCode(ea+7)
    else:
      if ea == 0x403A90:
        fcn_name = "NativeGRUNDTAL_NORRVIKEN"
        print "Defining fcn %s at 0x%x" % (fcn_name, ea)
      elif ea == 0x4044B0:
        fcn_name = "FYRKANTIGImpl"
        print "Defining fcn %s at 0x%x" % (fcn_name, ea)
      idc.MakeFunction(ea)
      idc.MakeNameEx(ea, fcn_name, idc.SN_NOWARN)

This was the main algo part implemented in the native functions, which were added at runtime. Incase you are wondering what does SPARSAM function does, so it just converts the list returned from these native functions to a string.

Z3 & Profit

Hell yeah! time for z3 as we are quite sure about how this challenge works :)
FYI, I’m not much experienced with z3 and it always has some surprises for me.

So at first I tried to just replicate the algo and check if it finds any valid solution. I initialized the input with the following constraints. 

1
s.add(And(inp[i]<=48, inp[i]>=125))

Then I add some If’s to encrypt our input so kinda do it all in z3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
  for i in range(len(inp)):
    inp[i] = If ( inp[i] - 48 <= 9,
          inp[i] - 48,
          inp[i])
    inp[i] = If ( inp[i] - 65 <= 25,
          inp[i] - 55,
          inp[i])
    inp[i] = If ( inp[i] - 97 <= 25,
          inp[i] - 61,
          inp[i])
    inp[i] = If ( inp[i] == 123,
          BitVecVal(62,32),
          inp[i])
    inp[i] = If ( inp[i] == 125,
          BitVecVal(63,32),
          BitVecVal(-1,32))
}

And I got UNSAT! :(
I asked for some help from my friends but the timezones messed up and I was determined enough to solve it myself now!

Finally I came up with an idea of removing just the z3 If statements and rather began with the encrypted input initially which had a range of (0, 63). And simply wrote a decrypt function for it. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def decode_inp(enc):
  dec = ""
  valid_range1 = ord('9') - ord('0')
  valid_range2 = ord('Z') - ord('0') - 7
  valid_range3 = ord('z') - ord('0') - (7+6)

  for c in enc:
    if c <= valid_range1:
      dec += chr(c + 48)
    elif c <= valid_range2:
      dec += chr(c + 55)
    elif c <= valid_range3:
      dec += chr(c + 61)
    elif c == 62:
      dec += '{'
    elif c == 63:
      dec += '}'

  return dec

WTH, Still UNSAT !!

drawing

And after spending some time tinkering around I figured out that it was some unsigned expressions shit in z3 which just made me mad (indescribable). 

1
2
s.add(UGE(MATHOPEN[29], 1))
s.add(ULE(MATHOPEN[0] + MATHOPEN[1] + MATHOPEN[2] + MATHOPEN[3] + MATHOPEN[4] - 130, 10))

In Z3Py, the operators <, <=, >, >=, /, % and >> correspond to the signed versions. The corresponding unsigned operators are ULT, ULE, UGT, UGE, UDiv, URem and LShR.

Reference :
https://ericpony.github.io/z3py-tutorial/guide-examples.htm

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
from z3 import *

def xor_mod(mod_list):
  xor_mask = [0x1F, 0x23, 0x3F, 0x3F, 0x1B, 0x07, 0x37, 0x21, 0x04, 0x33, 0x09, 0x3B, 0x39, 0x28, 0x30, 0x0C, 0x0E, 0x2E, 0x3F, 0x25, 0x2A, 0x27, 0x3E, 0x0B, 0x27, 0x1C, 0x38, 0x31, 0x1E, 0x3D]

  lol = []
  for i in range(len(mod_list)):
    lol.append(mod_list[i] ^ xor_mask[i])
  return lol


def get_checksum(mod_list):
  num = 16

  for i in range(len(mod_list)):
    if (i != len(mod_list) - 2):
      num = mod_list[i] + num

      if (i % 2 == 0):
        num = mod_list[i] + num
      
      if (i % 3 == 0):
        num = mod_list[i] * 4294967294 + num
      
      if (i % 5 == 0):
        num = mod_list[i] * 4294967293 + num
      
      if (i % 7 == 0):
        num = mod_list[i] * 4 + num
      
      num &= 0xffffffff

  return num & 63


def random_shuffle(arg_list):
  num_list = [0, 1, 0, 2, 3, 3, 7, 0, 6, 7, 7, 0, 3, 0xa, 0x6, 0xf, 0x3, 0x5, 0xc, 0xe, 0x3, 0x5, 0x8, 0x11, 0x17, 0x16, 0xa ]
  j = 1
  
  for i in num_list:
    if i != j:
      #print "Swapping :", (hex(arg_list[i]), hex(arg_list[j]) )
      #print "num =", hex(i)
      arg_list[i], arg_list[j] = arg_list[j], arg_list[i]
    #print i,j  
    j+=1

  return arg_list

def swap_more(arg_list):
  
  for j in range(0,len(arg_list)-3,3):
    arg_list[j], arg_list[j+1] = arg_list[j+1], arg_list[j]

  return arg_list

def decode_inp(enc):
  dec = ""
  valid_range1 = ord('9') - ord('0')
  valid_range2 = ord('Z') - ord('0') - 7
  valid_range3 = ord('z') - ord('0') - (7+6)

  for c in enc:
    if c <= valid_range1:
      dec += chr(c + 48)
    elif c <= valid_range2:
      dec += chr(c + 55)
    elif c <= valid_range3:
      dec += chr(c + 61)
    elif c == 62:
      dec += '{'
    elif c == 63:
      dec += '}'

  return dec


def final_conds(MATHOPEN, s):
  
  s.add(MATHOPEN[1] == 25)
  s.add(MATHOPEN[2] == 23)
  s.add(MATHOPEN[9] == 9)
  s.add(MATHOPEN[20] == 45)
  s.add(MATHOPEN[26] == 7)
  s.add(UGE(MATHOPEN[8], 15))
  s.add(ULE(MATHOPEN[12], 4))
  s.add(UGE(MATHOPEN[14], 48))
  s.add(UGE(MATHOPEN[29], 1))

  s.add(ULE(MATHOPEN[0] + MATHOPEN[1] + MATHOPEN[2] + MATHOPEN[3] + MATHOPEN[4] - 130, 10))
  s.add(ULE(MATHOPEN[5] + MATHOPEN[6] + MATHOPEN[7] + MATHOPEN[8] + MATHOPEN[9] - 140, 10))
  s.add(ULE(MATHOPEN[10] + MATHOPEN[11] + MATHOPEN[12] + MATHOPEN[13] + MATHOPEN[14] - 150 ,10)) 
  s.add(ULE(MATHOPEN[15] + MATHOPEN[16] + MATHOPEN[17] + MATHOPEN[18] + MATHOPEN[19] - 160 ,10)) 
  s.add(ULE(MATHOPEN[20] + MATHOPEN[21] + MATHOPEN[22] + MATHOPEN[23] + MATHOPEN[24] - 170 ,10)) 

  s.add(ULE(MATHOPEN[0] + MATHOPEN[5] + MATHOPEN[10] + MATHOPEN[15] + MATHOPEN[20] + MATHOPEN[25] - 172, 6)) 
  s.add(ULE(MATHOPEN[1] + MATHOPEN[6] + MATHOPEN[11] + MATHOPEN[16] +MATHOPEN[21] + MATHOPEN[26] - 162, 6)) 
  s.add(ULE(MATHOPEN[2] + MATHOPEN[7] + MATHOPEN[12] + MATHOPEN[17]+ MATHOPEN[22] + MATHOPEN[27] - 152, 6)) 
  s.add(ULE(MATHOPEN[3] + MATHOPEN[8] + MATHOPEN[13] + MATHOPEN[18] + MATHOPEN[23] - 142, 6)) 
  s.add(ULE(MATHOPEN[4] + MATHOPEN[9] + MATHOPEN[14] + MATHOPEN[19] + MATHOPEN[24] + MATHOPEN[29] - 132, 6)) 

  num45 = ((MATHOPEN[7] + (MATHOPEN[27] * 3)) * 3 - MATHOPEN[5] * 13) - 57
  s.add(ULE(num45, 28))
  
  num45 = (MATHOPEN[22] * 3 + ((MATHOPEN[14] << 2) - (MATHOPEN[20] * 5))) - 12
  s.add(ULE(num45, 70))

  num46 = (MATHOPEN[14] + (MATHOPEN[16] * 2)) * 2 + ((MATHOPEN[15] - ( MATHOPEN[18] * 2)) * 3) - MATHOPEN[17] * 5
  s.add(MATHOPEN[13] + num46 == 0)

  s.add(MATHOPEN[5] == MATHOPEN[6] * 2)
  s.add(MATHOPEN[29] + MATHOPEN[7] == 59)
  s.add(MATHOPEN[0] == MATHOPEN[17] * 6)
  s.add(MATHOPEN[8] == MATHOPEN[9] * 4)
  s.add(MATHOPEN[11] << 1 == MATHOPEN[13] * 3)
  s.add(MATHOPEN[13] + MATHOPEN[29] + MATHOPEN[11] + MATHOPEN[4] == MATHOPEN[19])
  s.add(MATHOPEN[10] == MATHOPEN[12] * 13)



def main():
  s = Solver()
  inp = []

  for i in range(30):
    b = BitVec("%d_i" % i, 32)
    inp.append(b)
    s.add(ULE(inp[i], 63))

  xor_res_list = xor_mod(inp)
  res1 = random_shuffle(xor_res_list)
  res2 = swap_more(res1)

  s.add(Distinct(res2))
  
  ret_num = get_checksum(res2)

  s.add(res2[28] == ret_num )

  final_conds(res2, s)

  print s.check()


  if s.check() == sat:
    sol = s.model()
    flag = []
    for i in range(len(inp)):
      c = inp[i]
      flag.append(int(str(sol[c])))
    print flag
    print decode_inp(flag)


if __name__ == "__main__":
  main()

1
2
3
sat
[12, 29, 15, 62, 12, 51, 51, 12, 47, 53, 18, 54, 32, 40, 44, 53, 39, 11, 56, 55, 27, 40, 36, 47, 47, 60, 15, 56, 49, 63]
CTF{CppClrIsWeirdButReallyFun}

Solution Files

I’ve uploaded all the files including the IDAPython and z3 solver scripts along with the idb file on my github here :

mrT4ntr4/Challenge-Solution-Files/GoogleCTF_2020_dotNet

I hope you liked this writeup :)
Well, Thanks for reading it…

STAY SAFE !

drawing